插入排序 概念 插入排序(InsertionSort),一般也被称为直接插入排序。
对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增 1 的有序表
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
说明 插入排序的平均时间复杂度也是 **O(n^2)**,空间复杂度为常数阶 **O(1)**,具体时间复杂度和数组的有序性也是有关联的。
插入排序中,当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较 N-1 次,时间复杂度为 **O(N)**。最坏的情况是待排序数组是逆序的,此时需要比较次数最多,最坏的情况是 **O(n^2)**。
过程演示 基本思想:每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插完所有元素为止。
上图为一动态例子
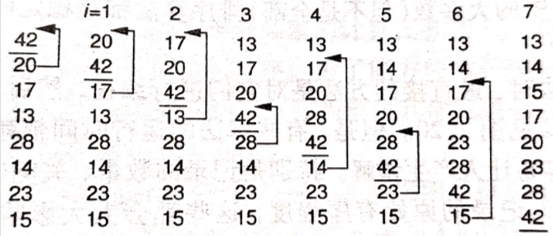
下面再举个书上的例子:对42,20,17,13,28,14,23,15进行插入排序(升序)
每次循环将比较该数与前面排好顺序的每个数进行比较,来决定这个数插入在哪个位置。
下面为java实现的代码(无使用swap函数)
public class InsertSort public void insertSort (int [] a) for (int i = 0 ; i < a.length; i++) { for (int j = 0 ; j < i; j++) { if (a[i] < a[j]){ int temp = a[i]; for (int k = i; k > j; k--) { a[k] = a[k-1 ]; } a[j] = temp; break ; } } } for (int i = 0 ; i < a.length; i++) { System.out.println(a[i]); } } public static void main (String[] args) InsertSort Obj = new InsertSort(); int [] test = new int [8 ]; test[0 ] = 42 ; test[1 ] = 20 ; test[2 ] = 17 ; test[3 ] = 13 ; test[4 ] = 28 ; test[5 ] = 14 ; test[6 ] = 23 ; test[7 ] = 15 ; Obj.insertSort(test); } }
冒泡排序 排序思想
基本思想: 冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来,假设从小到大,即为较大的数慢慢往后排,较小的数慢慢往前排。
直观表达,每一趟遍历,将一个最大的数移到序列末尾。
说明 冒泡排序的原理:每一趟只能确定将一个数归位,如果有n个数进行排序,只需将n-1个数归位,也就是说要进行n-1趟操作,而每一趟都需要从第1位开始进行相邻两个数的比较
过程演示
下面为Java实现的冒泡排序
import com.jiajia.ArrayUtil.*; public class BubbleSortMain private static void bubbleSort (int [] arr) if (arr==null || arr.length < 2 ){ return ; } for (int i = 0 ; i < arr.length - 1 ; i++) { for (int j = 0 ; j < arr.length - i -1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } } public static void main (String[] args) int [] arr = {2 ,5 ,1 ,3 ,8 ,5 ,7 ,4 ,3 }; bubbleSort(arr); ArrayUtil.print(arr); } }
选择排序 说明 选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度 。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
算法思想 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
过程演示
下面为Java实现的选择排序
public class SelectionSort implements IArraySort @Override public int [] sort(int [] sourceArray) throws Exception { int [] arr = Arrays.copyOf(sourceArray, sourceArray.length); for (int i = 0 ; i < arr.length - 1 ; i++) { int min = i; for (int j = i + 1 ; j < arr.length; j++) { if (arr[j] < arr[min]) { min = j; } } if (i != min) { int tmp = arr[i]; arr[i] = arr[min]; arr[min] = tmp; } } return arr; } }
希尔排序 排序思想 希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
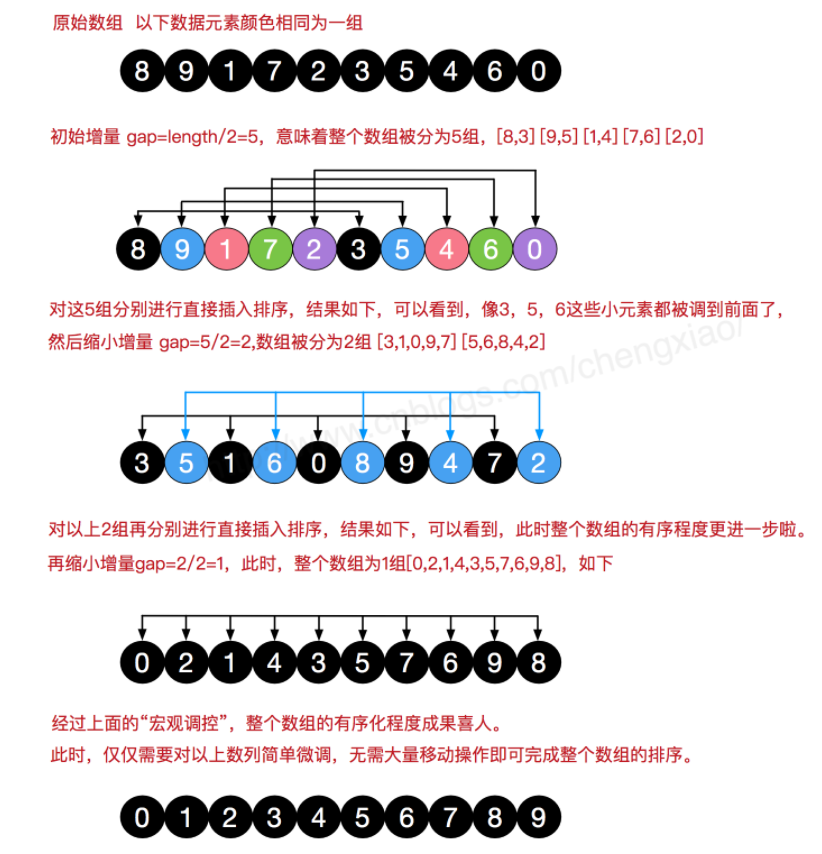
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录”基本有序”时,再对全体记录进行依次直接插入排序。
算法步骤 我们来看下希尔排序的基本步骤,我们通常选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列 。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。
过程演示
代码实现:
package sortdemo;import java.util.Arrays;public class ShellSort public static void main (String []args) int []arr ={1 ,4 ,2 ,7 ,9 ,8 ,3 ,6 }; sort(arr); System.out.println(Arrays.toString(arr)); int []arr1 ={1 ,4 ,2 ,7 ,9 ,8 ,3 ,6 }; sort1(arr1); System.out.println(Arrays.toString(arr1)); } public static void sort (int []arr) for (int gap=arr.length/2 ;gap>0 ;gap/=2 ){ for (int i=gap;i<arr.length;i++){ int j = i; while (j-gap>=0 && arr[j]<arr[j-gap]){ swap(arr,j,j-gap); j-=gap; } } } } public static void sort1 (int []arr) for (int gap=arr.length/2 ;gap>0 ;gap/=2 ){ for (int i=gap;i<arr.length;i++){ int j = i; int temp = arr[j]; if (arr[j]<arr[j-gap]){ while (j-gap>=0 && temp<arr[j-gap]){ arr[j] = arr[j-gap]; j-=gap; } arr[j] = temp; } } } } public static void swap (int []arr,int a,int b) arr[a] = arr[a]+arr[b]; arr[b] = arr[a]-arr[b]; arr[a] = arr[a]-arr[b]; } }