Haskell函数编程
简介
haskell 是一门纯函数式编程语言。
在命令式语言中执行操作需要给电脑安排一组命令,随着命令的执行,状态就会随之发生改变。例如你给变量 a 赋值为 5,而随后做了其它一些事情之后 a 就可能变成的其它值。有控制流程,你就可以重复执行操作。然而在函数式编程语言中,你不是像命令式语言那样命令电脑“要做什么”,而是通过用函数来描述出问题“是什么”,如“阶乘是指从1到某数间所有数字的乘积”。变量一旦赋值,就不可以更改了,你已经说了 a 就是 5,就不能再另说 a 是别的什么数。做人不能食言,对不?所以说,函数式编程语言中的函数能做的唯一事情就是求值,因而没有副作用。一开始会觉得这很受限,不过好处也正源于此:若以同样的参数调用同一函数两次,得到的结果总是相同。这被称作“引用透明”。如此一来编译器就可以理解程序的行为,你也很容易就能验证一个函数的正确性,继而可以将一些简单的函数组合成更复杂的函数。
类型
Haskell 是 Static Type—>编译时期每个表达式的型别都已经确定下来
各种类型(使用:t进行查看 )
与 Java 和 Pascal 不同,Haskell 支持型别推导。写下一个数字,你就没必要另告诉 Haskell 说”它是个数字”,它自己能推导出来。这样我们就不必在每个函数或表达式上都标明其型别了。
(配置好环境后在命令行中输入ghci)
ghci> :t 'a' |
:t 命令处理一个表达式的输出结果为表达式后跟 :: 及其型别,:: 读作”它的型别为”。凡是明确的型别,其首字母必为大写。'a', 如它的样子,是 Char 型别,易知是个字元 (character)。True 是 Bool 型别,也靠谱。不过这又是啥,检测 "hello" 得一个 [Char] 这方括号表示一个 List,所以我们可以将其读作”一组字元的 List”。而与 List 不同,每个 Tuple 都是独立的型别,于是 (True,'a') 的型别是 (Bool,Char),而 ('a','b','c') 的型别为 (Char,Char,Char)。4==5 一定回传 False,所以它的型别为 Bool
函数类型
函数也有型别。编写函数时,给它一个明确的型别声明是个好习惯,下面通过举例子来进行讲解
例如以下函数
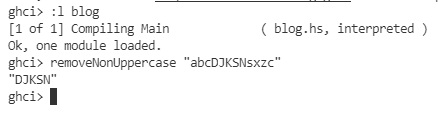
- 查找是否有大写字母
removeNonUppercase :: [Char] -> [Char] |
removeNonUppercase 的型别为 [Char]->[Char],从它的参数和回传值的型别上可以看出,它将一个字串映射为另一个字串。[Char] 与 String 是等价的,但使用 String 会更清晰:removeNonUppercase :: String -> String。编译器会自动检测出它的型别,我们还是标明了它的型别声明。
- 三个整数相加(多参数)
参数之间由 -> 分隔,而与回传值之间并无特殊差异。回传值是最后一项,参数就是前三项。稍后,我们将讲解为何只用 -> 而不是 Int,Int,Int->Int 之类”更好看”的方式来分隔参数。
如果你打算给你编写的函数加上个型别声明却拿不准它的型别是啥,只要先不写型别声明,把函数体写出来,再使用 :t 命令测一下即可。函数也是表达式,所以 :t 对函数也是同样可用的。
- 阶乘
factorial :: Integer -> Integer |
product为Haskell自带函数,及阶乘,后面可用递归来进行实现
Int 表示整数。7 可以是 Int,但 7.2 不可以。Int 是有界的,也就是说它由上限和下限。对 32 位的机器而言,上限一般是 2147483647,下限是 -2147483648。
Integer 表示…厄…也是整数,但它是无界的。这就意味着可以用它存放非常非常大的数,我是说非常大。它的效率不如 Int 高。
Haskell自带函数型别
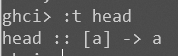
你觉得 head 函数的型别是啥?它可以取任意型别的 List 的首项,是怎么做到的呢?我们查一下!(使用:t)
- head
ghci> :t head |
嗯! a 是啥?型别吗?想想我们在前面说过,凡是型别其首字母必大写,所以它不会是个型别。它是个型别变数,意味着 a 可以是任意的型别。这一点与其他语言中的泛型 (generic) 很相似,但在 Haskell 中要更为强大。它可以让我们轻而易举地写出型别无关的函数。使用到型别变数的函数被称作”多态函数 “,head 函数的型别声明里标明了它可以取任意型别的 List 并回传其中的第一个元素。在命名上,型别变数使用多个字元是合法的,不过约定俗成,通常都是使用单个字元
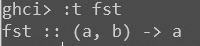
fst
ghci> :t fst
fst :: (a, b) -> a
可以看到fst取一个包含两个型别的 Tuple 作参数,并以第一个项的型别作为回传值。这便是 fst 可以处理一个含有两种型别项的 pair 的原因。注意,a 和 b 是不同的型别变数,但它们不一定非得是不同的型别,它只是标明了首项的型别与回传值的型别相同。
- Eq
ghci> :t (==) |
有意思。在这里我们见到个新东西:=> 符号。它左边的部分叫做型别约束。我们可以这样阅读这段型别声明:”相等函数取两个相同型别的值作为参数并回传一个布林值,而这两个参数的型别同在 Eq 类之中(即型别约束)”
Eq 这一 Typeclass 提供了判断相等性的介面,凡是可比较相等性的型别必属于 Eq class。
elem 函数的型别为: (Eq a)=>a->[a]->Bool。这是它在检测值是否存在于一个 List 时使用到了==的缘故。
- Ord(排序属性)
ghci> :t (>) |
型别若要成为Ord的成员,必先加入Eq家族。
Ord 包含可比较大小的型别。除了函数以外,我们目前所谈到的所有型别都属于 Ord 类。Ord 包中包含了<, >, <=, >= 之类用于比较大小的函数。compare 函数取两个 Ord 类中的相同型别的值作参数,回传比较的结果。这个结果是如下三种型别之一:GT, LT, EQ。
剩下的可以自己进行:t 查询返回结果 (Show,Enum,Bounded……)
函数语法
模式匹配 (Pattern matching)
本章讲的就是 Haskell 那套独特的语法结构,先从模式匹配开始。模式匹配通过检查数据的特定结构来检查其是否匹配,并按模式从中取得数据。
在定义函数时,你可以为不同的模式分别定义函数本身,这就让程式码更加简洁易读。你可以匹配一切数据型别 — 数字,字元,List,元组,等等。我们弄个简单函数,让它检查我们传给它的数字是不是 7。
lucky :: (Integral a) => a -> String |
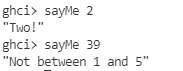
在呼叫 lucky 时,模式会从上至下进行检查,一旦有匹配,那对应的函数体就被应用了。这个模式中的唯一匹配是参数为 7,如果不是 7,就转到下一个模式,它匹配一切数值并将其绑定为 x 。这个函数完全可以使用 if 实现,不过我们若要个分辨 1 到 5 中的数字,而无视其它数的函数该怎么办?要是没有模式匹配的话,那可得好大一棵 if-else 树了!
sayMe :: (Integral a) => a -> String |
阶乘函数 递归实现
记得前面实现的那个阶乘函数么?当时是把 n 的阶乘定义成了 product [1..n]。也可以写出像数学那样的递回实现,先说明 0 的阶乘是 1 ,再说明每个正整数的阶乘都是这个数与它前驱 (predecessor) 对应的阶乘的积。如下便是翻译到 Haskell 的样子:
factorial :: (Integral a) => a -> a |
这就是我们定义的第一个递回函数。递回在 Haskell 中十分重要,我们会在后面深入理解。如果拿一个数(如 3)呼叫 factorial 函数,这就是接下来的计算步骤:先计算 3*factorial 2,factorial 2 等于 2*factorial 1,也就是 3*(2*(factorial 1))。factorial 1 等于 1*factorial 0,好,得 3*(2*(1*factorial 0)),递回在这里到头了,嗯 — 我们在万能匹配前面有定义,0 的阶乘是 1。于是最终的结果等于 3*(2*(1*1))。若是把第二个模式放在前面,它就会捕获包括 0 在内的一切数字,这一来我们的计算就永远都不会停止了。这便是为什么说模式的顺序是如此重要:它总是优先匹配最符合的那个,最后才是那个万能的。
模式匹配也会失败。假如这个函数:
charName :: Char -> String |
拿个它没有考虑到的字元去呼叫它,你就会看到这个:
ghci> charName 'a' |
它告诉我们说,这个模式不够全面。因此,在定义模式时,一定要留一个万能匹配的模式,这样我们的程序就不会为了不可预料的输入而崩溃了。
使用匹配模式来展示List前几项
弄个简单函数,让它用非标准的英语给我们展示 List 的前几项。
tell :: (Show a) => [a] -> String |
这个函数顾及了空 List,单元素 List,双元素 List 以及较长的 List,所以这个函数很安全。(x:[]) 与 (x:y:[]) 也可以写作 [x] 和 [x,y] (有了语法糖,我们不必多加括号)。不过 (x:y:_) 这样的模式就不行了,因为它匹配的 List 长度不固定。
什么是 Guards
模式用来检查一个值是否合适并从中取值,而 guard 则用来检查一个值的某项属性是否为真。咋一听有点像是 if 语句,实际上也正是如此。不过处理多个条件分支时 guard 的可读性要高些,并且与模式匹配契合的很好。
在讲解它的语法前,我们先看一个用到 guard 的函数。它会依据你的 BMI 值 (body mass index,身体质量指数)来不同程度地侮辱你。BMI 值即为体重除以身高的平方。如果小于 18.5,就是太瘦;如果在 18.5 到 25 之间,就是正常;25 到 30 之间,超重;如果超过 30,肥胖。这就是那个函数(我们目前暂不为您计算 BMI,它只是直接取一个 BMI 值)。
bmiTell :: (RealFloat a) => a -> String |
guard 由跟在函数名及参数后面的竖线标志,通常他们都是靠右一个缩进排成一列。一个 guard 就是一个布尔表达式,如果为真,就使用其对应的函数体。如果为假,就送去见下一个 guard,如之继续。如果我们用 24.3 呼叫这个函数,它就会先检查它是否小于等于 18.5,显然不是,于是见下一个 guard。24.3 小于 25.0,因此通过了第二个 guard 的检查,就返回第二个字串。
在这里则是相当的简洁,不过不难想象这在命令式语言中又会是怎样的一棵 if-else 树。由于 if-else 的大树比较杂乱,若是出现问题会很难发现,guard 对此则十分清楚。
最后的那个 guard 往往都是 otherwise,它的定义就是简单一个 otherwise = True ,捕获一切。这与模式很相像,只是模式检查的是匹配,而它们检查的是布尔表达式 。如果一个函数的所有 guard 都没有通过(而且没有提供 otherwise 作万能匹配),就转入下一模式。这便是 guard 与模式契合的地方。如果始终没有找到合适的 guard 或模式,就会发生一个错误。
当然,guard 可以在含有任意数量参数的函数中使用。省得用户在使用这函数之前每次都自己计算 bmi。我们修改下这个函数,让它取身高体重为我们计算。
bmiTell :: (RealFloat a) => a -> a -> String |
你可以测试自己胖不胖。
ghci> bmiTell 85 1.90 |
运行的结果是我不太胖。不过程式却说我很丑。
要注意一点,函数的名字和参数的后面并没有 =。许多初学者会造成语法错误,就是因为在后面加上了 =。
关键字 Where
前一节中我们写了这个 bmi 计算函数:
bmiTell :: (RealFloat a) => a -> a -> String |
注意,我们重复了 3 次。我们重复了 3 次。程式设计师的字典里不应该有”重复”这个词。既然发现有重复,那么给它一个名字来代替这三个表达式会更好些。嗯,我们可以这样修改:
bmiTell :: (RealFloat a) => a -> a -> String |
我们的 where 关键字跟在 guard 后面(最好是与竖线缩进一致),可以定义多个名字和函数。这些名字对每个 guard 都是可见的,这一来就避免了重复。如果我们打算换种方式计算 bmi,只需进行一次修改就行了。通过命名,我们提升了程式码的可读性,并且由于 bmi 只计算了一次,函数的执行效率也有所提升。我们可以再做下修改:
bmiTell :: (RealFloat a) => a -> a -> String |
函数在 where 绑定中定义的名字只对本函数可见,因此我们不必担心它会污染其他函数的命名空间。注意,其中的名字都是一列垂直排开,如果不这样规范,Haskell 就搞不清楚它们在哪个地方了。
where 绑定不会在多个模式中共享。如果你在一个函数的多个模式中重复用到同一名字,就应该把它置于全局定义之中。
where 绑定也可以使用模式匹配!前面那段程式码可以改成:
... |
递归
Maximum
现在看看递回的思路是如何:我们先定下一个边界条件,即处理单个元素的 List 时,回传该元素。如果该 List 的头部大于尾部的最大值,我们就可以假定较长的 List 的最大值就是它的头部。而尾部若存在比它更大的元素,它就是尾部的最大值。就这么简单!现在,我们在 Haskell 中实现它
maximum' :: (Ord a) => [a] -> a |
如你所见,模式匹配与递回简直就是天造地设!大多数命令式语言中都没有模式匹配,于是你就得造一堆 if-else 来测试边界条件。而在这里,我们仅需要使用模式将其表示出来。第一个模式说,如果该 List 为空,崩溃!就该这样,一个空 List 的最大值能是啥?我不知道。第二个模式也表示一个边缘条件,它说, 如果这个 List 仅包含单个元素,就回传该元素的值。
例子解析
我们取个 List [2,5,1] 做例子来看看它的工作原理。当呼叫 maximum' 处理它时,前两个模式不会被匹配,而第三个模式匹配了它并将其分为 2 与 [5,1]。 where 子句再取 [5,1] 的最大值。于是再次与第三个模式匹配,并将 [5,1] 分割为 5 和 [1]。继续,where 子句取 [1] 的最大值,这时终于到了边缘条件!回传 1。进一步,将 5 与 [1] 中的最大值做比较,易得 5,现在我们就得到了 [5,1] 的最大值。再进一步,将 2 与 [5,1] 中的最大值相比较,可得 5 更大,最终得 5。
改用 max 函数会使程式码更加清晰。如果你还记得,max 函数取两个值做参数并回传其中较大的值。如下便是用 max 函数重写的 maximun'
maximum' :: (Ord a) => [a] -> a |
太漂亮了!一个 List 的最大值就是它的首个元素与它尾部中最大值相比较所得的结果,简明扼要。
几个递回函数
- replicate
现在我们已经了解了递回的思路,接下来就使用递回来实现几个函数. 先实现下 replicate 函数, 它取一个 Int 值和一个元素做参数, 回传一个包含多个重复元素的 List, 如 replicate 3 5 回传 [5,5,5]. 考虑一下, 我觉得它的边界条件应该是负数. 如果要 replicate 重复某元素零次, 那就是空 List. 负数也是同样, 不靠谱.
replicate' :: (Num i, Ord i) => i -> a -> [a] |
在这里我们使用了 guard 而非模式匹配, 是因为这里做的是布林判断. 如果 n 小于 0 就回传一个空 List, 否则, 回传以 x 作首个元素并后接重复 n-1 次 x 的 List. 最后, (n-1) 的那部分就会令函数抵达边缘条件.
*Note*: Num 不是 Ord 的子集, 表示数字不一定得拘泥于排序, 这就是在做加减法比较时要将 Num 与 Ord 型别约束区别开来的原因. |
- take
接下来实现 take 函数, 它可以从一个 List 取出一定数量的元素. 如 take 3 [5,4,3,2,1], 得 [5,4,3]. 若要取零或负数个的话就会得到一个空 List. 同样, 若是从一个空 List中取值, 它会得到一个空 List. 注意, 这儿有两个边界条件, 写出来:
take' :: (Num i, Ord i) => i -> [a] -> [a] |
- reverse
reverse 函数简单地反转一个 List, 动脑筋想一下它的边界条件! 该怎样呢? 想想…是空 List! 空 List 的反转结果还是它自己. Okay, 接下来该怎么办? 好的, 你猜的出来. 若将一个 List 分割为头部与尾部, 那它反转的结果就是反转后的尾部与头部相连所得的 List.
reverse' :: [a] -> [a] |
继续下去!
Haskell 支持无限 List,所以我们的递回就不必添加边界条件。这样一来,它可以对某值计算个没完, 也可以产生一个无限的资料结构,如无限 List。而无限 List 的好处就在于我们可以在任意位置将它断开.
- repeat
repeat 函数取一个元素作参数, 回传一个仅包含该元素的无限 List. 它的递回实现简单的很, 看:
repeat' :: a -> [a] |
呼叫 repeat 3 会得到一个以 3 为头部并无限数量的 3 为尾部的 List, 可以说 repeat 3 运行起来就是 3:repeat 3 , 然后 3:3:3:3 等等. 若执行 repeat 3, 那它的运算永远都不会停止。而 take 5 (repeat 3) 就可以得到 5 个 3, 与 replicate 5 3 差不多.
“快速”排序
假定我们有一个可排序的 List, 其中元素的型别为 Ord Typeclass 的成员. 现在我们要给它排序! 有个排序算法非常的酷, 就是快速排序 (quick sort), 睿智的排序方法. 尽管它在命令式语言中也不过 10 行, 但在 Haskell 下边要更短, 更漂亮, 俨然已经成了 Haskell 的招牌了. 嗯, 我们在这里也实现一下. 或许会显得很俗气, 因为每个人都用它来展示 Haskell 究竟有多优雅!
它的型别声明应为 quicksort :: (Ord a) => [a] -> [a], 没啥奇怪的. 边界条件呢? 如料,空 List。排过序的空 List 还是空 List。接下来便是算法的定义:*排过序的 List 就是令所有小于等于头部的元素在先(它们已经排过了序), 后跟大于头部的元素(它们同样已经拍过了序)*。 注意定义中有两次排序,所以就得递回两次!同时也需要注意算法定义的动词为”是”什么而非”做”这个, “做”那个, 再”做”那个…这便是函数式编程之美!如何才能从 List 中取得比头部小的那些元素呢?List Comprehension。好,动手写出这个函数!
quicksort :: (Ord a) => [a] -> [a] |
测试
ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9] |
练习题
- 1
This task is meant to be solved with list comprehension.
Write a function headOrLast :: [String] -> Char -> [String] that, given a list of strings and a character, evaluates to a list with all the strings of the input list that either begin or end with the input character.
headOrLast :: [String] -> Char -> [String] |
- 2
This task is meant to be solved with guards.
We represent playing cards with (Char, Int) pairs. ‘s’ means spades, ‘h’ hearts, ‘c’ clubs’ and ‘d’ diamonds, with number values going from 2 to 14 (Ace being 14). Consider a game, where a player is dealt two cards and wins credits based on the following rules:
If the player has the Ace of Spades (‘s’, 14), then the player wins 6 credits.
Otherwise if the player has a pair (same number values), then the player wins 4 credits.
Otherwise if the player has two cards of the same suit, then the player wins 2 credits.
Otherwise, the player wins 0 credits.
Write a function credits :: (Char, Int) -> (Char, Int) -> Int that evaluates the given credits.
You can assume that the given cards are real
credits :: (Char, Int) -> (Char, Int) -> Int |
- 3
This task is meant to be solved with recursion.
Write a function nextIsGreater :: [Int] -> [Int] that, given a list of numbers, produces a list with all elements of the input list such that the element is followed by a greater number in the input list (the next number is greater).
The numbers need to be in the same order relative to each other in the output list as they are in the input list.
An example evaluation of the function:
function call:
nextIsGreater [0,5,2,3,2,2,3,1]
result:
[0,2,2]
nextIsGreater :: [Int] -> [Int] |
- 4
This task is suitable for a recursive solution.
We say that character pair (c1,c2) appears in string s with gap g, if c1 is before c2 and there are exactly g characters between c1 and c2 in s.
Write a function gap :: (Char, Char) -> Int -> String -> Int that, given a pair (c1,c2), a gap g and a string s returns an Int telling how many times (c1,c2) appear in s with gap g.
For example:
function call:
gap (‘a’,’b’) 1 “aaabbb”
result:
2
--4 |
- 5
Notice that e.g. length of a list is an Int and you can get a fractional (non-Integer) value out of that with the fromIntegral function.
Write a function distance1 :: String -> String -> Float that, given two strings s1 and s2, calculates their distance using the following formula ( (count of how many of the characters in s1 do not appear in s2 + (count of how many of the characters in s2 do not appear in s1) ) / ( (length of s1) + (length of s2) ). If both of the lists are empty, then the distance is 0.
For example, the distance between “aaabc” and “aabdd” with this function is (1 + 2) / (5 + 5).
Please note that this function is not standard well-behaving distance functions.
Hint: List comprehension is useful here.
--5 |
- 6
Write a function clusters that is given:
- f, a distance function of type String -> String -> Float (like the one in the previous Task 5)
- d :: Float
- ss :: [String]
For each string s in ss, the function clusters computes a “cluster”, ie a list of similar strings in ss (strings that are at most distance d from the s). The list of strings similar to s should also contain s (if the distance function allows).
The clusters and the list of clusters may be in any order.
Calling this function with function of Task 5, d=0.3 and ss=[“aaabc”, “aabdd”, “a”, “aa”, “abdd”, “bcbcb”, “”, “abcdefghij”]
should return
[[“”],[“a”,”aa”],[“a”,”aa”,”aaabc”],[“aa”,”aaabc”,”aabdd”,”bcbcb”],[“aaabc”,”aabdd”,”abdd”],[“aaabc”,”bcbcb”],[“aabdd”,”abdd”],[“abcdefghij”]]
(in some order).
--6 |