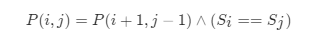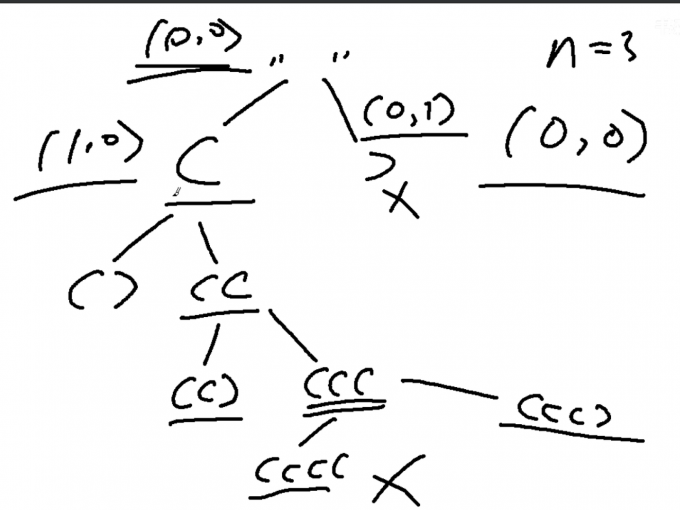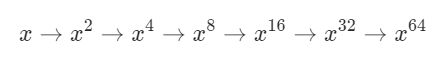1.两数相加（2）

数据结构

涉及数据结构： 单链表

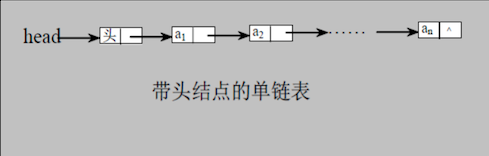
结构如下所示

WplRr6.png

注意：是逻辑结构，在内存中节点不是一个接一个的。

题解

思路

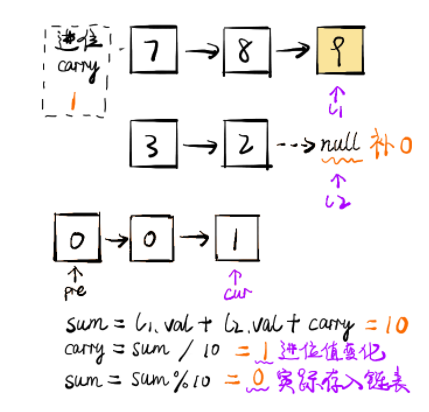
  • 将两个链表看成是相同长度的进行遍历，如果一个链表较短则在前面补 0，比如 987 + 23 = 987 + 023 = 1010。
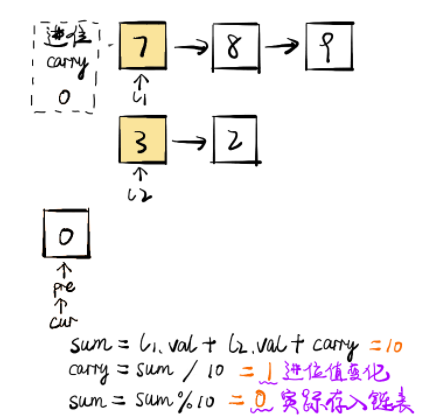
  • 每一位计算的同时需要考虑上一位的进位问题，而当前位计算结束后同样需要更新进位值
  • 如果两个链表全部遍历完毕后，进位值为 11，则在新链表最前方添加节点 11

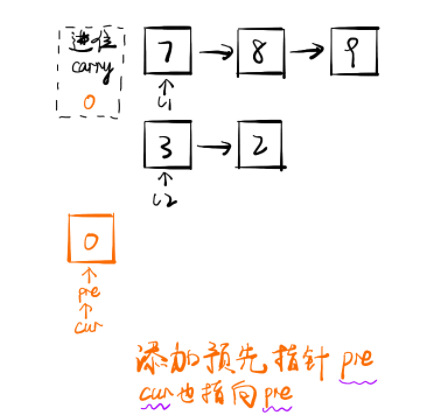
小技巧：对于链表问题，返回结果为头结点时，通常需要先初始化一个预先指针 pre，该指针的下一个节点指向真正的头结点head。使用预先指针的目的在于链表初始化时无可用节点值，而且链表构造过程需要指针移动，进而会导致头指针丢失，无法返回结果。

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode pre = new ListNode(0);
        ListNode cur = pre;
        int carry = 0;
        while(l1 != null || l2 != null) {
            int x = l1 == null ? 0 : l1.val;
            int y = l2 == null ? 0 : l2.val;
            int sum = x + y + carry;
            
            carry = sum / 10;
            sum = sum % 10;
            cur.next = new ListNode(sum);

            cur = cur.next;
            if(l1 != null)
                l1 = l1.next;
            if(l2 != null)
                l2 = l2.next;
        }
        if(carry == 1) {
            cur.next = new ListNode(carry);
        }
        return pre.next;
    }
}

链接：https://leetcode-cn.com/problems/add-two-numbers/solution/hua-jie-suan-fa-2-liang-shu-xiang-jia-by-guanpengc/

WCR7qI.png—>

WCW8JO.png—>

WCWUOA.png

2.无重复字符的最长字串（3）

数据结构

涉及数据结构： Map

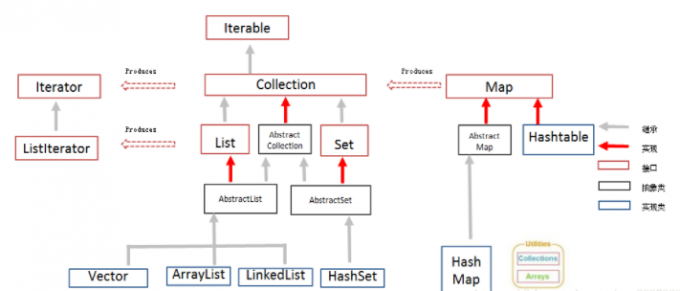
继承关系如下：

WC2DBt.md.png

  • Map中的集合，元素是成对存在的(理解为夫妻)。每个元素由键与值两部分组成，通过键可以找对所对应的值。
  • Map中的集合不能包含重复的键，值可以重复；每个键只能对应一个值。

Map有多个子类，这里我们主要讲解常用的HashMap集合、LinkedHashMap集合

  • **HashMap<K,V>**：存储数据采用的哈希表结构，元素的存取顺序不能保证一致。由于要保证键的唯一、不重复，需要重写键的hashCode()方法、equals()方法。

  • **LinkedHashMap<K,V>**：HashMap下有个子类LinkedHashMap，存储数据采用的哈希表结构+链表结构。通过链表结构可以保证元素的存取顺序一致；通过哈希表结构可以保证的键的唯一、不重复，需要重写键的hashCode()方法、equals()方法。

Map集合的功能概述

  • a:添加功能
    V put(K key,V value):添加元素。这个其实还有另一个功能?替换
    如果键是第一次存储，就直接存储元素，返回null
    如果键不是第一次存在，就用值把以前的值替换掉，返回以前的值
  • b:删除功能
    void clear():移除所有的键值对元素
    V remove(Object key)：根据键删除键值对元素，并把值返回
  • c:判断功能
    boolean containsKey(Object key)：判断集合是否包含指定的键
    boolean containsValue(Object value):判断集合是否包含指定的值
    boolean isEmpty()：判断集合是否为空
  • d:获取功能
    Set<Map.Entry<K,V>> entrySet(): 返回一个键值对的Set集合
    V get(Object key):根据键获取值
    Set keySet():获取集合中所有键的集合
    Collection values():获取集合中所有值的集合
  • e:长度功能
    int size()：返回集合中的键值对的对数

题解

思路
标签：滑动窗口

  • 暴力解法时间复杂度较高，会达到 O(n^2)，故而采取滑动窗口的方法降低时间复杂度。
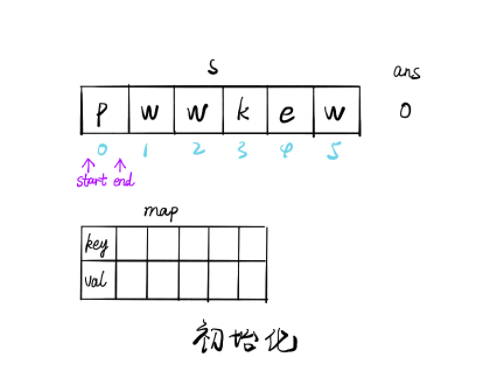
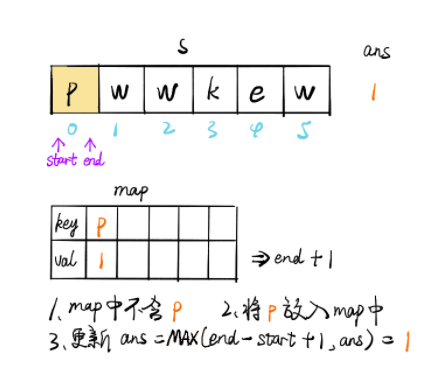
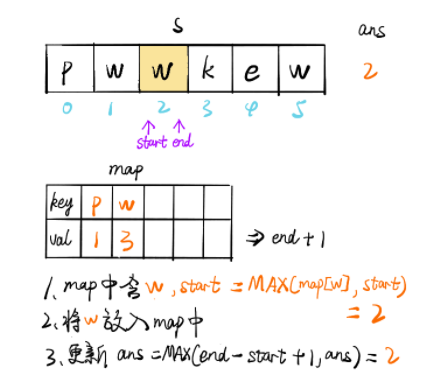
  • 定义一个 map 数据结构存储 (k, v)，其中 key 值为字符，value 值为字符位置 +1，加 1 表示从字符位置后一个才开始不重复。
  • 我们定义不重复子串的开始位置为 start，结束位置为 end。
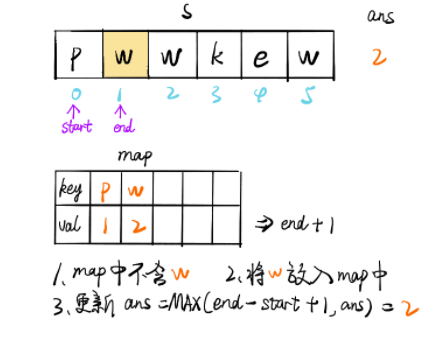
  • 随着 end 不断遍历向后，会遇到与 [start, end] 区间内字符相同的情况，此时将字符作为 key 值，获取其 value 值，并更新 start，此时 [start, end] 区间内不存在重复字符。
  • 无论是否更新 start，都会更新其 map 数据结构和结果 ans。
    时间复杂度：O(n)
public int solution(String s){
        int n = s.length(), ans = 0;
        Map<Character, Integer> map = new HashMap<>();  
        for (int end = 0, start = 0; end < n; end++) {
            char alpha = s.charAt(end); 
            if (map.containsKey(alpha)) {
                start = Math.max(map.get(alpha), start);
            }
            ans = Math.max(ans, end - start + 1);
            map.put(s.charAt(end), end + 1);
        }
        return ans;
}

WCHQw4.png—>

WCHN6K.png—>

WCHsfI.png—>

WCb8Hg.png—>

3.两数之和（1）

数据结构

涉及数据结构：数组和哈希表

特点

  • 哈希查找的时间复杂度为 O(1)**，所以可以利用哈希容器降低时间复杂度**

​ 哈希算法会根据你要存入的数据,先通过该算法,计算出一个地址值,这个地址值就是你需要存入到集合当中的数据的位置,而不会像数组那样一个个的进行挨个存 储,挨个遍历一遍后面有空位就存这种情况了,而你查找的时候,也是根据这个哈希算法来的,将你的要查找的数据进行计算,得出一个地址,这个地址会印射到集合当中的位置,这样就能够直接到这个位置上去找了,而不需要像数组那样,一个个遍历,一个个对比去寻找,这样自然增加了速度,提高了效率了。

​ 通过给定的关键字的值直接访问到具体对应的值的一个数据结构。也就是说，把关键字映射到一个表中的位置来直接访问记录，以加快访问速度。

  • 哈希表hashtable(key，value) 的做法其实很简单，就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里。

题解

1.暴力解法

public int[] solution(int[] nums, int target){
        int index = 0;
        int[] tar = new int[2];
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j <  nums.length; j++) {
                if(nums[i] + nums[j] == target){
                    tar[index] = i;
                    tar[index + 1] = j;
                    index += 2;
                }
            }
        }
        return tar;
    }

2. 哈希映射

思路

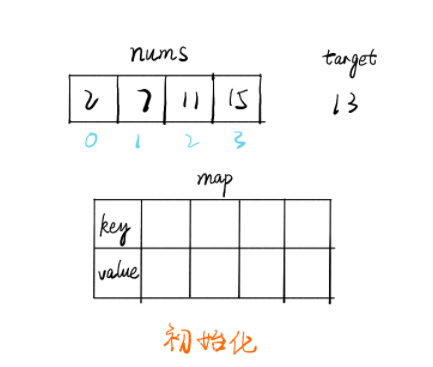
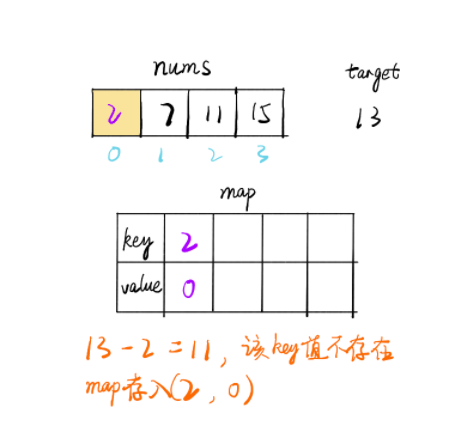
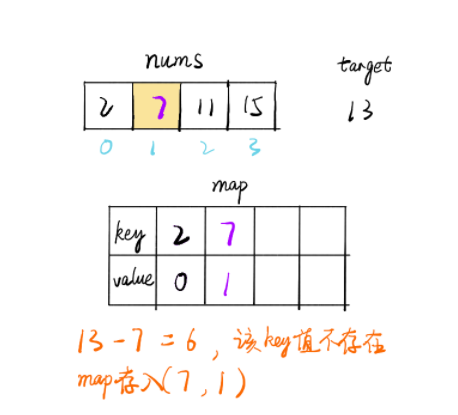
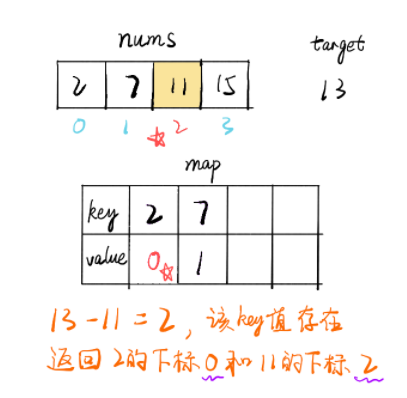
  • 遍历数组 nums，i 为当前下标，每个值都判断map中是否存在 target-nums[i] 的 key 值
  • 如果存在则找到了两个值，如果不存在则将当前的 (nums[i],i) 存入 map 中，继续遍历直到找到为止
public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i< nums.length; i++) {
            if(map.containsKey(target - nums[i])) {
                return new int[] {map.get(target-nums[i]),i};
            }
            map.put(nums[i], i);
        }
        throw new IllegalArgumentException("No two sum solution");
    }


链接：https://leetcode-cn.com/problems/two-sum/solution/jie-suan-fa-1-liang-shu-zhi-he-by-guanpengchn/

WFchcQ.png—>

WFgEge.png—>

WFgVjH.png—>

WFgnHI.png

4.最长回文子串（5）

数据结构

数组

题解

动态规划

思路

重点

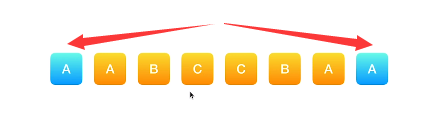
对于一个子串而言，如果它是回文串，并且长度大于2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串“ababa”，如果我们已经知道“bab”是回文串，那么“ababa”一定是回文串，这是因为它的首尾两个字母都是“a”。

WeEgOA.png

  • 根据这样的思路，我们就可以用动态规划的方法解决本题。我们用P(i,ij)表示字符串s的第i到j个字母组成的串(下文表示成s[i:j])是否为回文串:

WeVFmR.png

可以得出该题的状态方程如下

WeJrfH.png

WenpU1.md.png

public String longestPalindrome(String s) {
        int len = s.length();
        if(len < 2){
            return s;
        }

        int maxLen = 1;
        int begin = 0;

        boolean[][] dp = new boolean[len][len];
		//初始化
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        //左下角先填
        for (int j = 0; j < len; j++) {
            for (int i = 0; i < j; i++) {
                if(charArray[i] != charArray[j]){
                    dp[i][j] = false;
                }else{
                    if(j-i < 3){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                if(dp[i][j] && j - i + 1 >maxLen){
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin,begin + maxLen);
    }

5.字符串转换整数（8）

数据结构

数组

题解

思路：

  • 根据示例 1，需要去掉前导空格；
  • 根据示例 2，需要判断第 1 个字符为 + 和 - 的情况，因此，可以设计一个变量 sign，初始化的时候为 1，如果遇到 - ，将 sign 修正为 -1；
    判断是否是数字，可以使用字符的 ASCII 码数值进行比较，即 0 <= c <= ‘9’；
  • 根据示例 3 和示例 4 ，在遇到第 1 个不是数字的字符的情况下，转换停止，退出循环；
  • 根据示例 5，如果转换以后的数字超过了 int 类型的范围，需要截取。这里不能将结果 res 变量设计为 long 类型

注意：由于输入的字符串转换以后也有可能超过 long 类型，因此需要在循环内部就判断是否越界，只要越界就退出循环，这样也可以减少不必要的计算；
由于涉及下标访问，因此全程需要考虑数组下标是否越界的情况。

public int atoi(String str) {
        if (str == null || str.length() < 1)
            return 0;
// trim white spaces
        str = str.trim();
        char flag = '+';
// check negative or positive
        int i = 0;
        if (str.charAt(0) == '-') {
            flag = '-';
            i++;
        } else if (str.charAt(0) == '+') {
            i++;
        }
// use double to store result
        double result = 0;
// calculate value
        while (str.length() > i && str.charAt(i) >= '0' && str.charAt(i) <= '9') {
            result = result * 10 + (str.charAt(i) - '0');
            i++;
        }
        if (flag == '-')
        result = -result;
// handle max and min
        if (result > Integer.MAX_VALUE)
            return Integer.MAX_VALUE;
        if (result < Integer.MIN_VALUE)
            return Integer.MIN_VALUE;
        return (int) result;
    }

6.盛最多水的容器（11）

数据结构

涉及：数组，双指针用法

对于这道题

双指针解法的要点：指针每一次移动，都意味着排除掉了一个柱子

题解

思路：

  • 看下图，初始状况

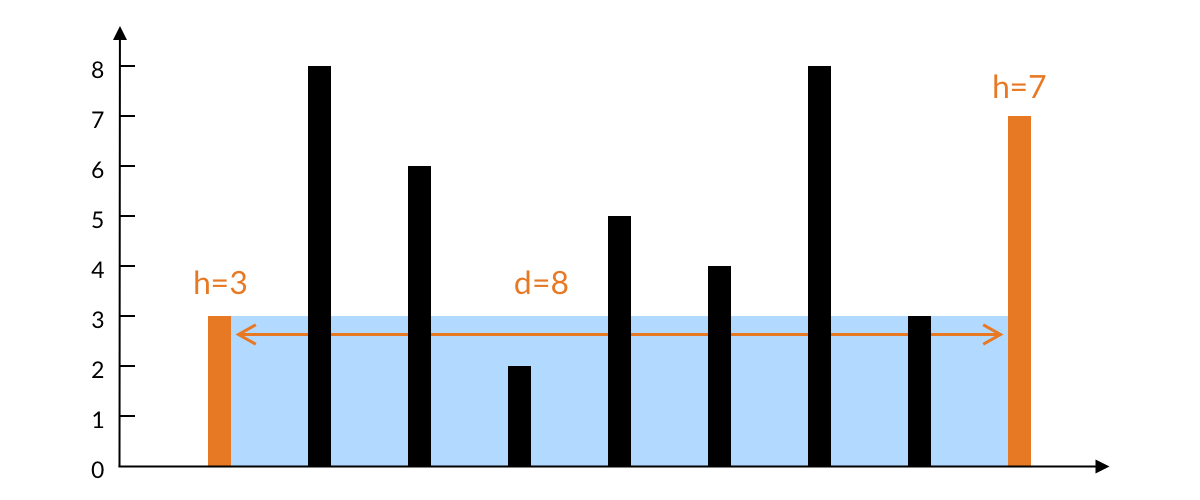
在一开始，我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 d = 8d=8；水的高度取决于两根柱子之间较短的那个，即左边柱子的高度 h = 3。水的面积就是 3 * 8 =24。

  • 如果选择固定一根柱子，另外一根变化，水的面积会有什么变化吗？思考可得：
    • 当前柱子是最两侧的柱子，水的宽度 d 为最大，其他的组合，水的宽度都比这个小
    • 左边柱子较短，决定了水的高度为 3。如果移动左边的柱子，新的水面高度不确定，一定不会超过右边的柱子高度 7。
      如果移动右边的柱子，新的水面高度一定不会超过左边的柱子高度 3，也就是不会超过现在的水面高度。

所以核心是：比较两边的柱子，移动小的柱子，并计算每次的面积并记录比较

public int maxArea(int[] height) {
        int res = 0;
        int i = 0;
        int j = height.length - 1;
        while (i < j) {
            int area = (j - i) * Math.min(height[i], height[j]);
            res = Math.max(res, area);
            if (height[i] < height[j]) {
                i++;
            } else {
                j--;
            }
        }
        return res;
    }

7.电话号码的字母组合

算法

涉及：回溯算法

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。

但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

一般步骤

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。

用回溯算法解决问题的一般步骤：

  • 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
  • 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
  • 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

WJcN26.md.png

思路

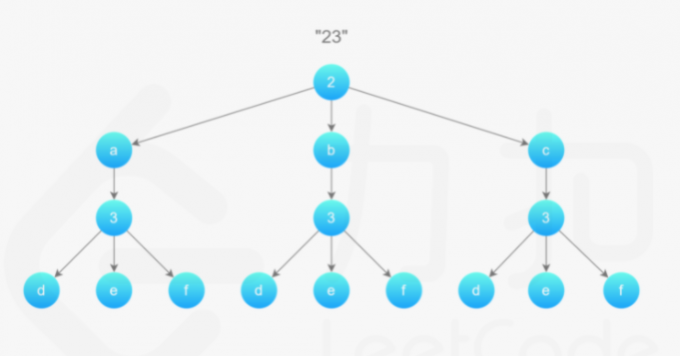
  • 首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作。

WJcxZ4.png

  • 回溯过程中维护一个字符串，表示已有的字母排列（如果未遍历完电话号码的所有数字，则已有的字母排列是不完整的）。该字符串初始为空。每次取电话号码的一位数字，从哈希表中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面，然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字，即得到一个完整的字母排列。然后进行回退操作，遍历其余的字母排列。

WJg70e.md.png

回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。在这道题中，由于每个数字对应的每个字母都可能进入字母组合，因此不存在不可行的解，直接穷举所有的解即可。

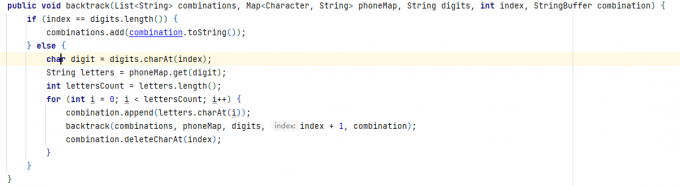
public List<String> letterCombinations(String digits) {
        List<String> combinations = new ArrayList<String>();
        if (digits.length() == 0) {
            return combinations;
        }
        Map<Character, String> phoneMap = new HashMap<Character, String>() {{
            put('2', "abc");
            put('3', "def");
            put('4', "ghi");
            put('5', "jkl");
            put('6', "mno");
            put('7', "pqrs");
            put('8', "tuv");
            put('9', "wxyz");
        }};
        backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
        return combinations;
    }

    public void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuffer combination) {
        if (index == digits.length()) {
            combinations.add(combination.toString());
        } else {
            char digit = digits.charAt(index);
            String letters = phoneMap.get(digit);
            int lettersCount = letters.length();
            for (int i = 0; i < lettersCount; i++) {
                combination.append(letters.charAt(i));
                backtrack(combinations, phoneMap, digits, index + 1, combination);
                combination.deleteCharAt(index);
            }
        }
    }

代码流程图

WJ2s3t.md.png

8.删除链表的倒数第 N 个结点（19）

数据结构

涉及：链表

题解

思路：

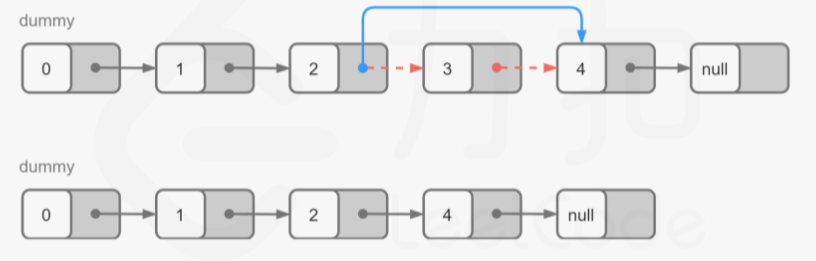
在对链表进行操作时，一种常用的技巧是添加一个哑节点（dummy node），它的 next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。

例如，在本题中，如果我们要删除节点 y，我们需要知道节点 y 的前驱节点 x，并将 x 的指针指向 y 的后继节点。但由于头节点不存在前驱节点，因此我们需要在删除头节点时进行特殊判断。但如果我们添加了哑节点，那么头节点的前驱节点就是哑节点本身，此时我们就只需要考虑通用的情况即可。

  • 首先得计算出链表的长度len

  • 将cur指针移动到删除节点前一个结点

public ListNode removeNthFromEnd(ListNode head, int n) {
        int len = 0;
        ListNode cur = head;
        while(cur != null){
            cur = cur.next;
            len ++ ;
        }
        ListNode dummy = new ListNode(0,head);
        cur = dummy;
        for (int i = 0; i < len - n; i++) {
            cur = cur.next;
        }
        cur.next = cur.next.next;
        return dummy.next;
}

f9uK1O.png

9.括号生成（22）

题解

算法：剪枝/回溯算法

fPN8VP.md.png

思路

  • 从空字符串开始（“ ”）来进行开始
  • 决定退出的条件:当左括号个数=n && 右括号个数=n，添加字符串
  • 剪枝条件：左括号个数 > n或左括号个数小于右括号个数

代码

public class GenerateParenthesis {
    ArrayList<String> list = new ArrayList<>();
    int n;

    public List<String> generateParenthesis(int n) {
        this.n = n;
        helper("",0,0);
        return list;

    }

    private void helper(String curr, int left, int right) {
        if(left == n && right ==n){
            list.add(curr);
        }

        if(left > n ||left < right){
            return;
        }
        helper(curr + "(" ,left + 1,right);
        helper(curr + ")" ,left,right + 1);
    }


    public static void main(String[] args) {
        GenerateParenthesis generateParenthesis = new GenerateParenthesis();
        System.out.println(generateParenthesis.generateParenthesis(3));
    }
}

10.两数相除（29）

位运算

1.位运算，左移一位是 * 2

2.位运算，右移一位是 / 2

题解

思路：

以10 /3 = 3为例

一般的思路为：

10-3-3-3

这种思路若被除数过大，会导致时间开销很大

所以可以简化为

10-3 * (2^0) -3 * (2^1) ……

以指数级的增长速度递增

(59条消息) leetcode29——两数相除——java实现_阿花的IT历程-CSDN博客

分析：
由于是有符号整数，所以我们要把正负情况都考虑进去。
为了简便运算，主体代码算的全是正的值，然后设置一个sign来表示正负号就可以了。

接下来主要看如何进行这个除法运算。
由于题目要求我们不能用乘法、除法、mod运算符，所以第一反应就是考虑位运算。

对于位运算，左移一位是*2，右移一位是/2.
在这里，我们要求的是它的商，可以这样考虑：
在被除数 >= 除数的条件下，令一个temp = 1,然后将除数左移一位，如果此时的除数 <= 被除数，则temp也左移一位，直到除数 > 被除数为止。

代码实现

class Solution {
    public int divide(int dividend, int divisor) {
        if(divisor == 0 || (dividend == Integer.MIN_VALUE && divisor == -1))
            return Integer.MAX_VALUE;
        int sign = (dividend < 0) ^ (divisor < 0) ? -1 : 1;
        long ldividend = (long)dividend;
        long ldivisor = (long)divisor;
        
        ldividend = Math.abs(ldividend);
        ldivisor = Math.abs(ldivisor);
        int count = 0;
        while(ldividend >= ldivisor) {
            long lds = ldivisor;
            long temp = 1;
            while((lds << 1) <= ldividend) {
                lds = (lds << 1);
                temp = (temp << 1);
            }
            count += temp;
            ldividend = ldividend - lds;
        }
        return count * sign;
    }
}

11.搜索旋转数组（33）

算法

关键词：有序数组

所以第一个想到的是二分查找

二分查找是一种查询效率非常高的查找算法。又称折半查找。

二分查找算法思想

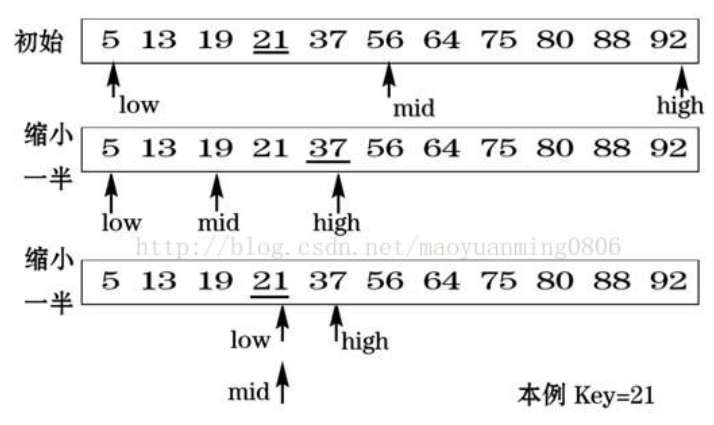
有序的序列，每次都是以序列的中间位置的数来与待查找的关键字进行比较，每次缩小一半的查找范围，直到匹配成功。

一个情景：将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

fVRnLd.png

题解

思路

对于有序数组，可以使用二分查找的方法查找元素。

但是这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。

可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：

  • 如果 [l, mid - 1] 是有序数组，且 target 的大小满足（nums[l]，nums[mid]） ，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
  • 如果 [mid, r] 是有序数组，且 target 的大小满足（nums[mid+1]，nums[r]），则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            if (nums[0] <= nums[mid]) {
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
}


12.有效数独(36)

题解

分析条件

  • 行中没有重复的数字。
  • 列中没有重复的数字。
  • 3 x 3 子数独内没有重复的数字。

解法（列出三个条件，三次循环，可以合并到一个循环中）

public class IsValidSudoku {
    public boolean isValidSudoku(char[][] board) {
        HashMap<Character, Integer> count = new HashMap<Character, Integer>();//存储每行或         每列或3*3的数据，并检查是否重复
        int times = 0;  //每3*3块的迭代次数
        int index = 0;  //3*3循环中行的增长速率
        int l = 0;    //3*3循环中列的增长速率
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length; j++) {
                if(count.containsKey(board[i][j])){
                    return false;
                }
                if(Character.isDigit(board[i][j])){
                    count.put(board[i][j],1);
                }
            }
            count.clear();//清空map
        }
        for (int i = 0; i < board[0].length; i++) {
            for (int j = 0; j < board.length; j++) {
                if(count.containsKey(board[j][i])){
                    return false;
                }
                if(Character.isDigit(board[j][i])){
                    count.put(board[j][i],1);
                }
            }
            count.clear();
        }
        while(true){
            if(times % 3==0 && times !=0){
                l++;
            }
            if(times % 3 == 0){
                index = 0;
            }
            for (int i = index  * 3; i <  3 * (index + 1); i++) {
                for (int j = l * 3; j < (l + 1) * 3; j++) {
                    if(count.containsKey(board[i][j])){
                        return false;
                    }
                    if(Character.isDigit(board[i][j])){
                        count.put(board[i][j],1);
                    }
                }
            }
            count.clear();  //清空3*3的map，进行下一次循环
            index++;
            times++;
            if(times == board.length){
                break;
            }
        }
        return true;
    }
}

13.全排列（46）

算法

回溯算法解题套路框架 :: labuladong的算法小抄 (gitee.io)

涉及算法：回溯算法

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」

题解

img

只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。

为啥说这是决策树呢，因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上：

img

你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的。

现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层，在这里就是选择列表为空的时候。

代码：

public class Permute {
    List<List<Integer>> res = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 1){
            List<Integer> temp = new LinkedList<>();
            temp.add(nums[0]);
            res.add(temp);
            return res;
        }
        LinkedList<Integer> track = new LinkedList<>();
        back(track, nums);
        return res;
    }
    void back(LinkedList<Integer> track, int[] nums){
        if (track.size() == nums.length){
            res.add(new LinkedList<>(track));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (track.contains(nums[i])){
                continue;
            }
            track.add(nums[i]);
            back(track, nums);
            track.removeLast();
        }
    }

    public static void main(String[] args) {
        Permute permute = new Permute();
        System.out.println(permute.permute(new int[]{1,2,3,6}));
    }
}

14.解码方法（91）

算法/题解

涉及算法：动态规划

思路：

这题可以想象成爬楼梯的升级版，加上腿酸不酸的条件（如果get不到可以忽视这句，捂脸）首先转移方程其实挺容易想的，就是边界条件想半天（吐槽）f(n)=f(n-1)+f(n-2)就是转移方程了。why？不考虑边界情况下，第n个字符可以自己独立进行解码，或者与n-1组合成两位数进行解码，所以f(n)=f(n-1)+f(n-2)。
接下来就是考虑边界条件，首先什么情况下可以加上f(n-1)？根据前面说的可以自己独立解码时，那什么时候不加？就是不能独立解码，为0时。ok，完成一半了。
什么情况下可以加上f(n-2)？根据前面说的n与n-1组成两位数并且可以解码，好！根据这句话可以得到，首先能是两位数，这是一个条件。并且可以解码，所以charAt(n-1)*10+charAt(n)得是两位数，并且<=26.还有一个可能会忽略的。得是两位数！什么情况下不会得到两位数？charAt(n-1) = 0,所以还有一个条件就是charAt(n-1) 不能为0.

public class NumDecodings {
    public int numDecodings(String s) {
        int n = s.length();
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            if (s.charAt(i - 1) != '0') {
                f[i] += f[i - 1];
            }
            if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
                f[i] += f[i - 2];
            }
        }
        return f[n];
    }

    public static void main(String[] args) {
        NumDecodings numDecodings = new NumDecodings();
        System.out.println(numDecodings.numDecodings("226"));
    }
}

15.矩阵置零（73）

算法/题解

使用标记数组

分析：

我们可以用两个标记数组分别记录每一行和每一列是否有零出现。

具体地，我们首先遍历该数组一次，如果某个元素为 0，那么就将该元素所在的行和列所对应标记数组的位置置为 \text{true}true。最后我们再次遍历该数组，用标记数组更新原数组即可。

class Solution {
    
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean[] row = new boolean[m];
        boolean[] col = new boolean[n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    row[i] = col[j] = true;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (row[i] || col[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

16.二叉树的层序遍历（102）

数据结构

涉及：二叉树

定义
满二叉树：在满二叉树中除叶子结点外的内部结点，都有两个非空的子结点
完全二叉树：从根节点开始，每一层按照从左到右的顺序依次水平填充树，叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部

性质
非空二叉树上的叶子结点数等于度为2的结点数加1，即n0 = n2 + 1

非空二叉树第k层上至多有2k-1个结点（k>=1）

具有n（n>0）个结点的完全二叉树的高度为 ⌊log2n⌋+1 或 ⌈log2n+1⌉

存储
顺序存储
用一组连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素

对于一棵完全二叉树，这样存储的好处是数组下标直接对应某个结点。可以根据性质找到其双亲或孩子结点。

对于一棵非完全二叉树，添加一个不存在的空结点，在数组中可以用0表示

弊端：顺序存储最坏情况下会非常浪费存储空间，比较适合完全二叉树

遍历

按某条路径访问树中的每个结点，树的每个结点均被访问一次

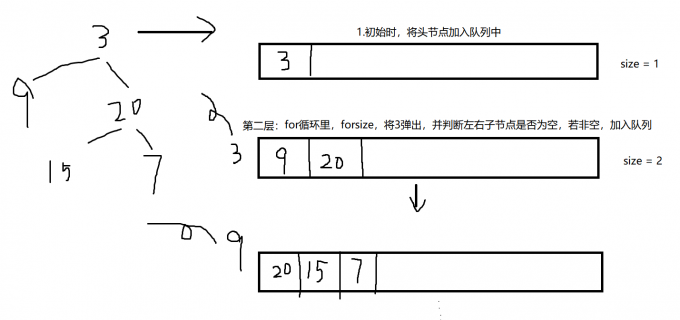
题解

算法思想：

  1. 初始将根入队并访问根结点，然后出队
  2. 如有左子树，则将左子树的根入队
  3. 如有右子树，则将右子树的根入队
  4. 然后出队，访问该结点
  5. 反复该过程直至队列为空

图示：

fUfr0U.md.png

按照该图，写出代码:

public class LevelOrder {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList<List<Integer>> res = new ArrayList<List<Integer>>();
        Queue<TreeNode> eve = new LinkedList<>();
        if(root == null){
            return null;
        }
        eve.add(root);
        while(!eve.isEmpty()){
            ArrayList<Integer> integers = new ArrayList<>();
            int size = eve.size();
            for (int i = 0; i < size; i++) {
                TreeNode curr = eve.poll();
                integers.add(curr.val);
                if(curr.left != null){
                    eve.add(curr.left);
                }
                if(curr.right != null) {
                    eve.add(curr.right);
                }
            }
            res.add(integers);
        }
        return res;
    }
}

17.验证二叉搜索树（98）

题解

public class IsValidBST {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 访问左子树
        if (!isValidBST(root.left)) {
            return false;
        }
        // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。
        if (root.val <= pre) {
            return false;
        }
        pre = root.val;
        // 访问右子树
        return isValidBST(root.right);
    }
}

18. Pow(x,n) (50)

题解

快速幂 + 递归

如果我们要计算 x^64，我们可以按照：

frElVJ.png

的顺序，从 xx 开始，每次直接把上一次的结果进行平方，计算 6 次就可以得到 x^{64} 的值，而不需要对 x乘 63 次 x。

frEqMT.md.png

public class MyPow {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }


    public static void main(String[] args) {
        System.out.println(new MyPow().myPow(2, 3));
    }
}

19.子集

算法

设计算法：回溯

题解

public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> allSubsets = new ArrayList<>();
        List<Integer> tempsubset = new ArrayList<>();
        for(int size =  0;size <= nums.length; size ++){
            backtrack(0,size,tempsubset,allSubsets,nums);
        }
        return allSubsets;
    }

    private void backtrack(int index ,int size,List<Integer> tempsubset,List<List<Integer>> allSubsets,int[] nums){
        if(tempsubset.size() == size){
            allSubsets.add(new ArrayList<>(tempsubset));
            return;
        }

        for(int i = index;i < nums.length;i++){
            tempsubset.add(nums[i]);
            backtrack(i + 1,size,tempsubset,allSubsets,nums);
            tempsubset.remove(tempsubset.size() - 1);
        }
    }

20.加油站

题解

一次遍历法，车能开完全程需要满足两个条件：

  • 车从i站能开到i+1。
  • 所有站里的油总量要>=车子的总耗油量。

那么，假设从编号为0站开始，一直到k站都正常，在开往k+1站时车子没油了。这时，应该将起点设置为k+1站。

问题1: 为什么应该将起始站点设为k+1？

  • 因为k->k+1站耗油太大，0->k站剩余油量都是不为负的，每减少一站，就少了一些剩余油量。所以如果从k前面的站点作为起始站，剩余油量不可能冲过k+1站。

问题2: 为什么如果k+1->end全部可以正常通行，且rest>=0就可以说明车子从k+1站点出发可以开完全程？

  • 因为，起始点将当前路径分为A、B两部分。其中，必然有(1)A部分剩余油量<0。(2)B部分剩余油量>0。
  • 所以，无论多少个站，都可以抽象为两个站点（A、B）。(1)从B站加满油出发，(2)开往A站，车加油，(3)再开回B站的过程。

重点：B剩余的油>=A缺少的总油。必然可以推出，B剩余的油>=A站点的每个子站点缺少的油。

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int rest = 0, run = 0, start = 0;
        for (int i = 0; i < gas.length; ++i){
            run += (gas[i] - cost[i]);
            rest += (gas[i] - cost[i]);
            if (run < 0){
                start = i + 1;
                run = 0;
            }
        }
        return rest < 0 ? -1: start;
    }
}